Räkning med ensiffriga tal
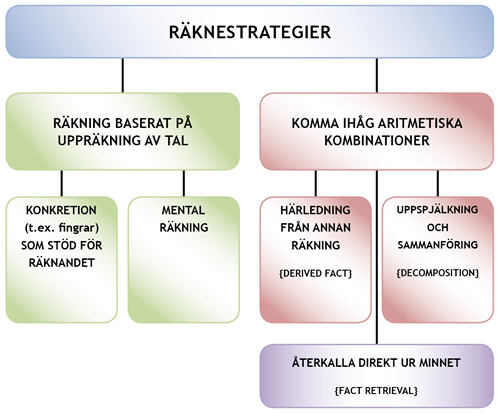
Generell utveckling av aritmetiska färdigheter
Utvecklingen av de aritmetiska färdigheterna i addition, subtraktion, multiplikation och division kan beskrivas via användningen av olika räknestrategier (t.ex. Baroody, 1984; Fennema, Carpenter, Jacobs, Franke & Levi, 1998; Fuson, 1984; Geary, Bow-Thomas, Liu & Siegler, 1996), eftersom användningen av räknestrategierna återspeglar en utvecklingsmässig ordningsföljd. Som en led i utvecklingen av räknefärdigheterna lär sig barnet nya räknestrategier och kan samtidigt lämna någon tidigare inlärd strategi bakom sig. Utvecklingen av räknefärdigheterna kan beskrivas utgående från den relativa andelen av olika strategier som barnet använder, t.ex. genom att följa med i vilken mån barnet återkallar svar från minnet och i vilken mån lösningen erhålls med uppräkning.
Det är skillnad mellan olika räkneoperationer gällande hur stor mängd av inlärningen som präglas av att använda svar ur minnet eller av olika räknestrategier. T.ex. när det gäller att lära sig multiplikationstabellerna är utantillinlärning den oftast förekommande strategin eftersom svaren i regel hämtas ur minnet. Däremot är utantillkunskapen inte en avgörande strategi när det gäller subtraktion eller division, utan där krävs användning av särskilda räknestrategier som stöds av addition och multiplikation.
Barnet använder ofta flera räknestrategier också inom de enskilda räkneoperationerna. Valet av strategi påverkas av faktorer i uppgiften. Redan i förskolåldern kan barnet utantill kunna svaret till flera ”små” räkneoperationer vars svar är under 10. Däremot är räkneoperationer som kräver tiotalsövergång (8 + 7, 6 + 9) betydligt svårare och även äldre barn måste ty sig till att räkna istället för använda färdigt inlärda svar. Sådana aritmetiska räkneoperationer som innehåller 1 eller 0 (t.ex. 4 + 0 eller 6 x 0) avviker i valet av strategier så till vida att inlärningen verkar bygga rätt långt på att känna till en regel, som t.ex. att ”om man adderar eller subtraherar en nolla, är svaret samma tal”.
Strategierna som barnet använder får man reda på genom att följa med barnets räknande och be barnet förklara hur han eller hon har löst uppgiften. Vanligen använder sig barnet av flera olika strategier. Barn som räknar flytande kännetecknas av att de i huvudsak snabbt återkallar svaret från minnet, men kan också vid behov välja den effektivaste strategin. De barn som har inlärningssvårigheter i matematik använder sig ofta enbart av långsamma strategier som baserar sig på uppräkning. Lösningsmodeller som bygger på att komma ihåg aritmetiska kombinationer är därför svåra för dessa barn. Undersökningar visar att svårigheter att lära sig och att komma ihåg aritmetiska kombinationer är relativt bestående till sin karaktär och svårigheterna försvinner inte av sig själva med åldern, utan särskilda stödåtgärder krävs. Barnet behöver stöd av de vuxna för att läsa sig snabbare och effektivare räknestrategier (se avsnittet om stödåtgärder).
Utveckling av färdigheter i addition och subtraktion
Färdigheterna i addition och subtraktion utvecklas stegvis. Räknefärdigheten utvecklas från att baseras på uppräkning till att komma ihåg aritmetiska kombinationer. Barnet använder sig av och provar rätt spontant de olika strategierna, och lär sig dem via undervisning i skolan (Steinberg, 1985; Thornton, 1978; Thornton 1990). Strategier för subtraktion är svårare för barn än strategier för addition - såväl när det gäller spontan inlärning som gällande inlärningen i skolan (Steinberg, 1985). Subtraktion kräver att man håller flera saker i minnet än vid addition. Användningen av subtraktionsstrategier underlättas av att sambandet mellan addition och subtraktion förstås.
Addition och subtraktion baserat på uppräkning av talraden
Till en början löser barnet räkneuppgifter med hjälp av strategier som grundar sig på uppräkning. Barnet räknar med hjälp av konkret och visuellt stöd (t.ex. föremål, fingrar och genom att rita) för att så småningom övergå till att använda uppräkning av talraden enbart som mental räkning (Ostad, 1999; Siegler & Shrager, 1984; Siegler, 1987). I användningen av denna strategi kan även urskiljas hur barnet räknar vid uppräkning, dvs. hur många tal som räknas upp och från vilket tal barnet börjar.
I det första skedet räknar barnet alla räkneoperationens delmoment en åt gången med föremål eller med fingrar och likaså med svaret (t.ex. 2 + 4 räknas 1, 2 ― 1, 2, 3, 4 ― 1, 2, 3, 4, 5, 6). Senare, då färdigheterna utvecklats, räknar barnet från mitten av talraden (så att 2 + 4 räknas 2 ― 3, 4, 5, 6). I detta skede har barnets färdigheter som berör talraden utvecklats så att uppräkning kan starta mitt i talraden. Ett tecken på att ett effektivare sätt att räkna är att barnet räknar upp så få tal som möjligt, t.ex. genom att börja uppräkningen från det högsta talet (2 + 4 blir 4, 5, 6). Det är bra att tillsammans med barnet gå igenom principen om kommutativitet (dvs. att ordningsföljden inte spelar någon roll när man räknar ihop tal t.ex. 2 + 4 = 4 + 2) så att barnet kan lära sig dra nytta av detta i sitt räknande. I subtraktion förutsätter användningen av samma strategi sambandet med addition. Exempelvis i räkneoperationen 9 - 7 är det snabbare att räkna framåt från sju till nio (åtta, nio, svaret är 2) än att räkna baklänges från nio (åtta, sju, sex, fem, fyra, tre, två). När barnet inte längre använder sig av föremål som konkret stöd för räknandet, måste barnet hålla flera saker i minnet samt information om hur många som lagts till eller tagits bort och komma ihåg vilket steg utgör själva svaret (t.ex. i 5 + 3 tänker man ”ett till är sex, två till är sju, tre till är åtta”).
Att mentalt lösa räkneuppgifter med hjälp av strategier som baseras på uppräkning är således en prestation med flera steg. En förutsättning för att lösa räkneuppgifterna är att barnet klarar av flera simultana processer och att hålla flera saker i minnet samtidigt. Därför är det viktigt att barnet utan problem kan räkna upp talraden fram- och baklänges med start från ett givet tal (Baroody, 1984).
Räkning som baseras på uppräkning av talraden är mödosamt, långsamt och har en stor benägenhet att bli fel. Barnet använder trots det fingrarna som stöd för räknandet, tills färdigheterna har utvecklats så att barnet kan räkna enbart mentalt och senare snabbt återkalla aritmetiska kombinationer ur minnet.
Addition baserat på uppräkning av talraden
|
räknar alla, börjar från början |
T.ex. 3 + 2 = ? Barnet räknar tre föremål ett i sänder "1,2,3". Adderar två föremål genom att räkna "1,2", räknar sedan alla föremål från början "1,2,3,4,5" och får resultatet fem. |
|
räknar ena talet, börjar från början |
T.ex. 3 + 4 = ? Barnet visar direkt talet tre med fingrarna och räknar upp fyra tal till ”1, 2, 3, 4". Sen räknar han alla fingrar på nytt från början för att få svaret som är alla fingrarna tillsammans. |
|
räknar framåt |
T.ex. 4 + 3 = ? Barnet visar talet 4 med fingrarna och räknar framåt med hjälp av fingrarna "5, 6, 7". Svaret är det sist nämnda räkneordet. |
|
räknar framåt, börjande från högsta talet |
T.ex. 2 + 5 = ? Barnet påbörjar räknandet från det högsta talet. Talet 5 visas med fingrarna och därefter lägger man till två fingrar "6, 7". Svaret är det sist nämnda räkneordet. |
|
räknar framåt från det första talet |
T.ex. 3 + 4 = ? Barnet börjar från talet 3 och räknar i tanken framåt "4, 5, 6, 7". Svaret är det senast nämnda räkneordet.
|
|
räknar framåt från det största talet |
T.ex. 2 + 5 = ? Barnet påbörjar räknandet vid det största talet, säger talet 5 och räknar i tanken framåt "6, 7". Svaret är det sistnämnda räkneordet. |
Subtraktion baserat på uppräkning av talraden
|
räknar alla, börjar från början |
T.ex. 5 – 3 = ? Barnet räknar fem föremål ett i sänder. Sen räknar det bort tre föremål, räknar de kvarvarande ett i sänder och får resultatet två. |
|
räknar framåt |
T.ex. 7 – 4 = ? Barnet börjar från talet 4, räknar framåt med hjälp av fingrarna ”5, 6, 7”. Svaret är antalet uppräknade räkneord, dvs. 3. |
|
räknar baklänges givet antal steg |
T.ex. 8 – 3 = ? Barnet påbörjar räknandet från 8 och räknar med hjälp av fingrarna tre steg bakåt ”7, 6, 5”. Svaret är det sist nämnda talet. |
|
räknar fram- eller baklänges |
Barnet väljer att använda antingen det andra eller tredje av de ovan givna alternativen, beroende på vilket kräver mindre räkning. |
|
räknar framåt |
T.ex. 7 – 4 = ? Barnet börjar från talet 4, räknar framåt i huvudet ”5, 6, 7”. Antalet uppräknade tal utgör svaret, alltså tre. |
|
räknar bakåt givet antal steg |
T.ex. 8 – 3 = ? Barnet påbörjar räkningen vid 8 och räknar i huvudet tre steg bakåt ”7, 6, 5”. Svaret är det sist uttalade talet. |
|
räknar bakåt till givet tal |
T.ex. 8 - 6 =? Barnet börjar med 8 och räknar i tanken stegvis till 6 "7, 6". Svaret är de uppräknade talens antal, dvs. 2. |
|
räknar bak- eller framlänges |
Barnet väljer något av de ovannämnda alternativen så att det behövs så lite räkning som möjligt. T.ex. i 9 - 7 = ?, kunde barnet välja det första eller tredje alternativet ovan. |
Memorering av aritmetiska kombinationer vid addition och subtraktion
När barnet framgångsrikt använder sig av räknestrategierna för addition och subtraktion stärks förståelsen för sambandet mellan uträkningens delmoment och svar. (Barrouillet & Fayol, 1998; Siegler & Shrager, 1984). Barnet lär sig att direkt memorera räkneuppgiftens svar ur minnet (t.ex. 2 + 3 = 5). Barnet kan också använda de inlärda aritmetiska kombinationerna vid lösning av räkneuppgifter. Barnet kan härleda tidigare kunskap om någon kombination som behärskas (t.ex. att 6 – 3 = 3 och därför är 6-4 =2, eftersom talet fyra är ett större än tre). Barnet kan också spjälka upp uträkningen i delar och sammanföra den på nytt genom att använda kombinationer han eller hon redan kan, t.ex. kan 7 + 5 = ? spjälkas upp i 7 + (3 + 2), som underlättar räkningen (10 + 2 = 12).
Enligt vissa forskare (bl.a. Putnam m.fl., 1990; Thornton, 1990; Carpenter & Moser, 1984) kan härledning via en annan räkneuppgift främja inlärning av aritmetiska kombinationer och direkt återerinring från minnet. Man kan t.ex. först lära barnet s.k. dubbelpar (att addera två likadana tal, t.ex. 4 +4) som är lätta att komma ihåg och att använda dessa som stöd vid närliggande aritmetiska kombinationer (som 4 + 4 = 8, och därför är 4 + 5 = 9). Att härleda via andra uträkningar och att dela upp uppgiften kan i början åskådliggöras för barnet med hjälp av konkret och visuellt material.
I allmänhet lär sig barn att utnyttja memorerade kombinationer som sin huvudsakliga räknestrategi redan i ungefär nio års ålder. (Ashcraft & Fierman, 1982; Brauwer, Verguts, & Fias, 2006; Lemair & Siegler, 1995). När barnet använder mera utvecklade räknestrategier återkallas resultatet snabbt ur minnet (ca 2-3 sekunder). Dessa aritmetiska kombinationer som återkallas direkt ur minnet kan barnet använda som stöd i sådana uppgifter till vilka han eller hon inte ännu har svar. När stora tal räknas med uppställning blir det ännu viktigare att komma ihåg de enkla uträkningarna utantill. Om räknandet inte är flytande inom talområdet 0-20, blir räkning med uppställningen en långsam process. Att behärska talområdet 0-20 flytande är en förutsättning för att kunna räkna stora tal.
Härledning från annan uträkning vid addition
|
dubblering +1, +2 |
Man använder sig av ett tidigare känt dubbelpar och adderar ett eller två. |
|
dubblering -1, -2 |
Man använder sig av ett tidigare känt dubbelpar och subtraherar ett eller två. |
|
tioparen |
Man använder tidigare inlärda tiopar. |
|
10-räkning |
Man använder tioräkning, där en term innehåller talet tio. |
|
delning |
Additionen konkretiseras med klossar genom att man flyttar en kloss från en hög till en annan så att man får dubbelpar. Denna inre bild kan man ha nytta av i räkning. |
|
via annan känd kombination |
T.ex. 7+5=(7+4)+1=12 |
Härledning från annan uträkning vid subtraktion
|
dubblering +1 |
Man använder sig av redan kända dubbelpar och adderar ett. |
|
dubblering -1 |
Man använder sig av redan kända dubbelpar och subtraherar ett. |
|
delning |
Additionen konkretiseras enkelt med klossar genom att man flyttar en kloss från en hög till en annan utgående för att få dubbelpar. Denna inre bild kan man ha nytta av i subtraktion. |
|
10-räkning |
Man använder sig av tioräkning, där en term är talet tio. |
|
via annan känd kombination |
T.ex. 12 - 7 --> 12 - 8 = 4, alltså 12 - 7 = 5 |
Uppspjälkning och sammanföring vid addition
|
addition via 10 |
Talet fylls på först till tio och därefter ser man hur många som ännu kommer till över tio. |
Uppspjälkning och sammanföring vid subtraktion
|
addition via 10 |
Talet fylls på först till tio och därefter ser man hur många som blir kvar över tio. |
|
subtraktion via 10 |
Talet minskas först till 10. Därefter tar man bort det som blivit över från tio. |
|
minskning från tio |
Man tar ”vara på” den del av talet som är över 10. Efter det subtraheras termen från 10 och därefter adderas talet man tagit till vara i början. |
Sätten för att undervisa additionsstrategier
Sätten för att undervisa subtraktionsstrategier
Utveckling av färdigheter i multiplikation och division
Multiplikation avviker från addition och subtraktion i det avseendet att inlärningsprocessen tydligare följer ett rakt spår och att man i övningen betonar främst utantillinlärning. En vanlig utveckling av räknefärdigheter i multiplikation är att redan från början hämta svaret ur minnet.
Av de aritmetiska operationerna är division den klart minst undersökta. I början verkar barnen använda sig av upprepad addition, men så småningom blir multiplikation snabbt det mest använda sättet att lösa divisionsuppgifter. Det centrala för utvecklingen av färdigheterna i division är att behärska multiplikationen bra och att förstå sambandet mellan multiplikation och division. Att lösa divisionsuppgifter i praktiken blir tungt och svårt om barnet inte behärskar multiplikation. Detta är viktigt att komma ihåg när man väljer var man börjar när räknefärdigheter ska stödas.
Multiplikation och division baserat på uppräkning av talraden
I det tidiga skedet i inlärningen av multiplikation använder barnen som strategi rätt allmänt upprepad addition eller uppräkning av talraden i steg. En del av barnen kan genom att räkna högt eller enbart mentalt röra sig längs med tallinjen utan visuellt stöd, t.ex. med fem steg i taget (t.ex. 4 x 5 räknas 5, 10, 15, 20). Barnen kan även använda sina fingrar som stöd i uppräkningen för att komma ihåg hur många steg som tagits (”fem” motsvaras av ett finger, ”tio” av två, osv.). En del av barnen kan inte röra sig längs med tallinjen i steg, utan blir tvungna att lösa multiplikationerna genom att räkna dem en och en. Barnet kan t.ex. rita grupper av streck och räkna dem. Att lösa multiplikationer genom att räkna streck är inte meningsfullt och i sådana fall gäller det främst att stöda barnets färdigheter gällande talraden och addition, samt att klargöra multiplikationens begrepp.
Till de strategier som baserar sig på uppräkning kan för divisionens del nämnas upprepad addition, där nämnaren räknas ihop tills man når täljaren, samt subtraktion där man räknar bort nämnaren från täljaren tills man når noll. En strategi som lite påminner om detta är gruppering, där barnet avgör hur många grupper som är lika stora som nämnaren. Antalet grupper anger mängden (täljaren) som ska delas.
Memorering av aritmetiska kombinationer vid multiplikation och division
Den vanligaste strategin att lösa multiplikation är att hämta de aritmetiska kombinationerna direkt ur minnet. Internationella studier har visat att den vanligaste räknestrategin vid multiplikation redan bland andraklassister är att återhämta svaren ur minnet, och det använder barnen i över hälften av multiplikationsuppgifterna. På fjärde klass (i 9 års ålder) löser barnen uppgifterna till största delen (70-80%) genom att använda sig enbart av minnet.
En annan strategi som baseras på minnet är härledning från andra tal.
För divisionens del är minnesbaserade strategierna att hämta svaret direkt ur minnet, att räkna med hjälp av multiplikation samt att spjälka upp räkneuppgiften i mindre uträkningar som är lättare att lösa. Av de fyra räknesätten verkar division vara det räknesätt som ”allra minst blir automatiserad” hos barnen. En kanadensisk studie visade att även lite äldre elever (årskurs 6-7) betydligt mer sällan använde sig av minnet än av multiplikation som strategi i division.


